LENGTH OF COMMON TANGENT BETWEEN TWO CIRCLES / GARIS SINGGUNG LINGKARAN : PERSEKUTUAN DALAM DAN LUAR
Length of the Common External and Internal Tangent between Two Circles Calculator.
Kalkulator Mencari panjang Garis Singgung persekutuan dalam dan luar antara dua Lingkaran.
The Formula Length of the Common internal tangent between Two Circle is following below:
Rumus Untuk mencari panjang garis singgung persekutuan dalam dua lingkaran adalah sebagai berikut:
For Example / Contoh:
Circle a has a radius of 4cm and Circle b has a radius of 11cm. If the distance between the center of the circle in 17cm, find the length of the common internal tangent.
Panjang jari-jari Lingkaran a adalah 4cm dan lingkaran b panjang jari-jarinya adalah 11cm. Jika jarak kedua pusat lingkaran tersebut adalah 17cm. Tentukanlah panjang garis singgung perseketuan luarnya!
Solution / Jawaban:
r = 4
R = 11
p = 17
$d=\sqrt{p^2-(R+r)^2}$
Kalkulator Mencari panjang Garis Singgung persekutuan dalam dan luar antara dua Lingkaran.
Input value of the Radius [R and r] and Distance between centres [p].
Masukkan panjang jari-jari [R dan r] dan jarak antara pusat lingkaran [p]
The Formula Length of the Common internal tangent between Two Circle is following below:
Rumus Untuk mencari panjang garis singgung persekutuan dalam dua lingkaran adalah sebagai berikut:
$d=\sqrt{p^2-(R+r)^2}$
d = Length of the Common Internal tangent / Panjang garis singgung persekutuan dalam.
p = Distance between Centres / Jarak antara pusat lingkaran.
R = Radius of Big Circle / Jari-jari lingkaran Besar.
r = Radius of Small Circle / Jari-jari lingkaran kecil.
For Example / Contoh:
Circle a has a radius of 4cm and Circle b has a radius of 11cm. If the distance between the center of the circle in 17cm, find the length of the common internal tangent.
Panjang jari-jari Lingkaran a adalah 4cm dan lingkaran b panjang jari-jarinya adalah 11cm. Jika jarak kedua pusat lingkaran tersebut adalah 17cm. Tentukanlah panjang garis singgung perseketuan luarnya!
Solution / Jawaban:
r = 4
R = 11
p = 17
$d=\sqrt{p^2-(R+r)^2}$
Ss$=\sqrt{17^2-(11+4)^2}$
Ss$=\sqrt{289-225}$
Ss$=\sqrt{64}$
Ss$=8$
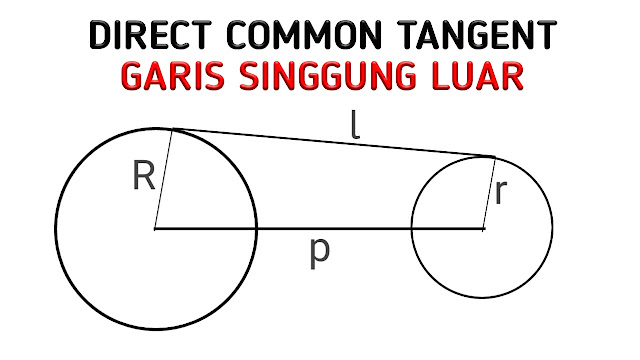
The Formula of the Length of the Common external tangent between Two Circle is following below:
Rumus Untuk mencari panjang garis singgung persekutuan luar dua lingkaran adalah sebagai berikut:
For Example / Contoh:
Two circle of radii 3cm and 8cm. If the distance between the center of the circle in 13cm, find the length of the common external tangent.
Dua buah lingkaran mempunyai jari-jari 3cm dan 8cm. Jika jarak pusat lingkaran adalah 13cm, tentukanlah panjang garis singgung persekutuan luarnya!
Solution / Jawaban:
r = 3
R = 8
p = 13
$l=\sqrt{p^2-(R-r)^2}$
The Formula of the Length of the Common external tangent between Two Circle is following below:
Rumus Untuk mencari panjang garis singgung persekutuan luar dua lingkaran adalah sebagai berikut:
$l=\sqrt{p^2-(R-r)^2}$
l = Length of the Common External tangent / Panjang garis singgung persekutuan luar.
p = Distance between Centres / Jarak antara pusat lingkaran.
R = Radius of Big Circle / Jari-jari lingkaran Besar.
r = Radius of Small Circle / Jari-jari lingkaran kecil.
For Example / Contoh:
Two circle of radii 3cm and 8cm. If the distance between the center of the circle in 13cm, find the length of the common external tangent.
Dua buah lingkaran mempunyai jari-jari 3cm dan 8cm. Jika jarak pusat lingkaran adalah 13cm, tentukanlah panjang garis singgung persekutuan luarnya!
Solution / Jawaban:
r = 3
R = 8
p = 13
$l=\sqrt{p^2-(R-r)^2}$
S$=\sqrt{13^2-(8-3)^2}$
S$=\sqrt{169-25}$
S$=\sqrt{144}$
S$=12$


Belum ada Komentar untuk "LENGTH OF COMMON TANGENT BETWEEN TWO CIRCLES / GARIS SINGGUNG LINGKARAN : PERSEKUTUAN DALAM DAN LUAR"
Posting Komentar